Roll Dice Like A Computer: A Pseudo-Random Journey
Like Oil and Water
It’s easy to take randomness for granted, especially because we live in such a chaotic world! With a flip of the coin, you’ve generated a truly random result. For computers, it’s not that easy.
Computers follow strict rules which are the opposite of random. So how do computers generate randomness? The short answer is: they don’t. Rather, your computer does the next best thing which is to generate pseudo-random numbers. Read pseudo as “pretend” random numbers. A set of fixed rules and instructions create these numbers not randomness. These instructions make up what we call a random number generator or RNG for short.

With an RNG, a computer is able to now utilize randomness for applications like shuffling a playlist of songs or randomizing a deck of virtual cards on a gambling website.
Today we’ll take a look at what randomness looks like and how we can make our own pseudo-random numbers.
What Does Randomness Look Like?
Fairness
To understand how computers generate random numbers, we first need to understand what exactly we want from a sequence of numbers.
I’ll roll a 6-sided die a hundred times and see how the results spread out.
| Dice Roll | Number of times Rolled |
|---|---|
| 1 | 9 |
| 2 | 11 |
| 3 | 12 |
| 4 | 11 |
| 5 | 9 |
| 6 | 8 |
We notice that despite being random, the average number of rolls for each number is about 10. Counting 10 out of 60 total rolls is in line with what everyone knows intuitively: there is a \(\frac{1}{6}\) chance for each side to be rolled.
This reveals something we want from our random number generator. We want our RNG to be fair and generate different numbers with the same probability. Imagine playing Monopoly against someone who keeps rolling 6’s. Not very fun huh?

No Patterns
It’s not enough to be able to generate different numbers at equal parts. The numbers have to also look as random as possible. Imagine if I told my computer to roll virtual dice and it outputted the following results:
- 1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6
This would pass our previous criterion of being fair. However, the results are clearly not random. To appear random means that no obvious patterns should emerge.
Let’s compare our “dummy” computer to actual dice rolls.
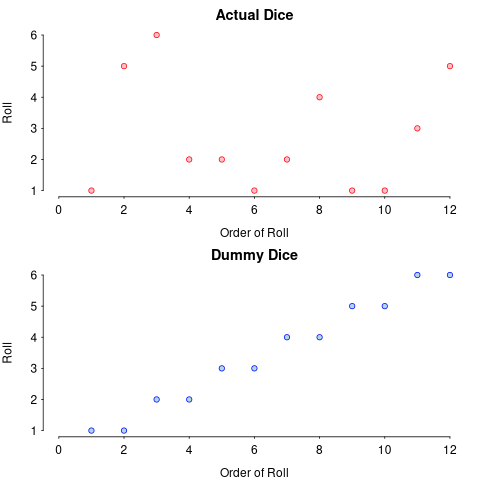
As we can see from our actual dice rolls, there is no discernable pattern over time. That first plot is something we want from our random number generator.
So all in all, our two main criteria for our random number generator is:
- Each roll is fair
- There are no discernable patterns over time
Introducing the Middle Square Method
One of the earliest random number generators is called the “middle-square method”. The method creates random numbers from 0 to 9999.
- Pick a “seed” number from 0 to 9999
- Square that seed number.
- Remove 2 digits from both sides. The result is your new number
Might be a bit to take in but it’s best understood with an example. For step 1 I’ll choose 5832 as my seed number.
Step 2
\[ 5832 * 5832 = 34012224 \]
Step 3
\[ \sout{34}0122\sout{24} = 0122 \]
122 is our random number.
If we want to make more new numbers we can go back to step 1 using 122 as our new seed!
\[ 122 * 122 = 00014884 \]
\[ \sout{00}0148\sout{84} = 0148 \]
So far we’ve had a sequence of 5832, 122, and 148. Let’s see what happens if we keep doing this 50 times.
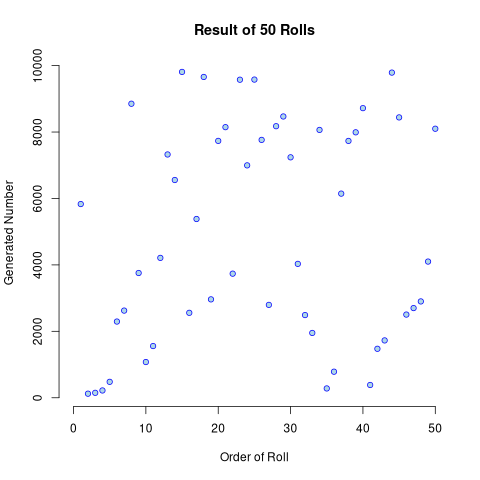
Seems pretty random to me!
What About the Dice Roll?
How do we simulate a dice roll out of this? Unless we’re in need of a 10000-sided die, this doesn’t seem to be very useful.
All we need to do is to split 10000 into 6 roughly equal parts:
- 0 to 1667
- 1668 to 3333
- 3334 to 5000
- 5001 to 6667
- 6668 to 8333
- 8334 to 10000
If a number falls into the first part it will be like rolling a 1. If a number falls into the second part it will be like rolling a 2. So on and so forth.
Let’s plot the rolls against real dice.
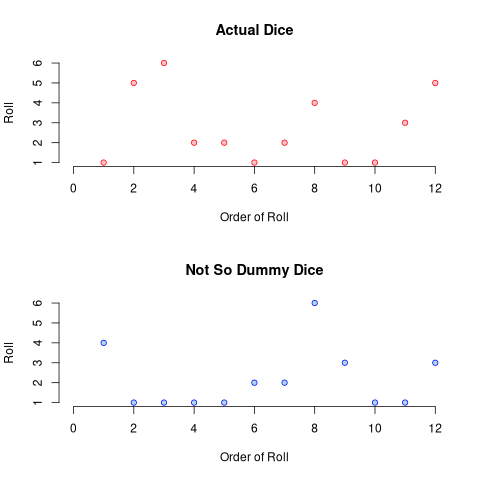
Our dice rolls seem just as random as actual dice. How are the rolls distributed?
| Dice Roll | Num of Times Rolled - Virtual Die | Num of Times Rolled - Actual Die |
|---|---|---|
| 1 | 10 | 9 |
| 2 | 14 | 11 |
| 3 | 7 | 12 |
| 4 | 7 | 11 |
| 5 | 13 | 9 |
| 6 | 9 | 8 |
If we compare our virtual die to our actual die that we rolled earlier, they both revolve closely to 10. Our new virtual dice roller works wonders. Hopefully, you’ve come out of this realizing that even you can roll dice similar to a computer!